Результаты и задачи математического конкурса за 2015 год
Победители конкурса 2015 года.

Задачи и результаты конкурса прошлых лет: 2014, 2013, 2012
X тур

46.(Дима Ботин) Хулиган Семён, любимое число которого – семь, забрался ночью через окно в гостиницу «Караван-Сарай» и с дверей всех номеров снял семёрки. Утром Семёна поймал полицейский Пронькин, который заявил, что за каждую снятую цифру полагается платить штраф в размере одного доллара. Сколько долларов придётся заплатить Семёну, если в гостинице 1000 номеров и они нумеруются подряд, начиная с 1?
47.(Дима Ботин) Ученик Рома, который любит рисовать, начертил на асфальте треугольник. Ученик Вова, который любит измерять высоты треугольников, заметил, что у начерченного Ромой треугольника все высоты меньше 1 см. Ученик Петя, который любит измерять периметр фигур, обнаружил, что периметр треугольника Ромы больше 2000 см. Учительница Марьиванна, услышав это, заявила, что кто-то из ребят наверняка соврал. Права ли Марьиванна?

48.(Сергей Федин)
У питона Капитона
Вес четыре с лишним тонны.
Мается питон от колик,
Лишнее – костлявый кролик,1
В килограммах весит он,
Сколько в тоннах Капитон.
Сколько весили в тот вечер
Кролик и питон ДО встречи?2
1То есть вес питона больше четырёх тонн как раз на вес кролика.
2Всё, о чём говорится в первых шести строчках стихотворения, происходит ПОСЛЕ встречи, то есть кролик находится уже внутри питона.
49.(Александр Шаповалов) Имеется 18 прямоугольников размером 2x1. Проведите в каждом из них одну из диагоналей и сложите из получившихся прямоугольников квадрат размером 6x6 так, чтобы концы диагоналей нигде не совпали.


50. Двадцать сосисок и десять сарделек соединены в цепочку в произвольном порядке. Две собаки хотят перекусить цепочку в нескольких местах соединений так, чтобы можно было поделить получившиеся части поровну (по десять сосисок и пять сарделек каждой собаке). Какого наименьшего количества перекусываний им заведомо хватит?
IX тур

41.(Дмитрий Шноль) Даны 5 карточек, на них написаны дроби 1⁄2, 1⁄3, 1⁄4, 1⁄5, 1⁄6. Можно использовать некоторые (или все) карточки, знаки арифметических действий и скобки. Получите таким способом все целые числа от 0 до 10.

42. Загаданы четыре целых числа a, b, c, d. Разрешается выбрать любые три из них и спросить: их сумма чётная или нечётная? Как за три таких вопроса узнать, чётно или нечётно число a?

43. На Поле Чудес растут два дерева. Если закопать несколько золотых под одним из них, то к утру сумма удвоится, а если под другим – утроится. У Буратино есть 100 золотых, но он не знает, какое из деревьев удваивает сумму, а какое – утраивает. К утру у него должно быть ровно 175 золотых. Как ему этого добиться? (Он не обязан закапывать все свои золотые.)

44.(Игорь Акулич)
Имеется шахматная доска, у которой первоначально все клетки белые. Закрасим некоторые из них в чёрный цвет. Назовём раскраску изящной, если в каждой горизонтали и каждой вертикали закрашено ровно по 4 клетки (то есть обычная шахматная раскраска тоже изящная).
Возьмём две произвольные изящные раскраски. Петя уверен, что если разрешить менять местами любые две горизонтали или любые две вертикали, то, совершив несколько таких операций, можно из первой раскраски получить вторую. Коля считает, что это не так. Кто прав?

45.(Лейб Штейнгарц)
На плоскости отметили несколько точек, никакие три из которых не лежат на одной прямой. Сколько точек могли отметить, если известно, что любой треугольник с вершинами в отмеченных точках будет непременно
а) остроугольным;
б) прямоугольным;
в) тупоугольным?
Найдите все ответы и докажите, что других нет.
VIII тур

36. В поход пошли 10 человек, младше всех остальных был Гриша. Он нашёл сумму возрастов остальных участников похода и поделил на сумму возрастов всех десяти человек. Мог ли Гриша получить число меньше, чем 0,9?
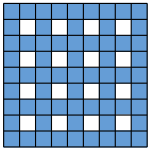
37.(Павел Кожевников) Разрежьте нарисованную слева синюю клетчатую фигуру на несколько клетчатых прямоугольников так, чтобы среди них было как можно меньше квадратиков из одной клетки.

38.(Алексей Толпыго, Александр Шаповалов)
Квантик и Ноутик показывают такой фокус. Зритель задумывает любые два разных целых числа от 1 до 25 и сообщает их только Ноутику.
После этого Ноутик называет Квантику какие-то другие два целых числа от 1 до 25 (отличные от задуманных), и Квантик тут же угадывает задуманные зрителем числа.
Предложите способ, как могли бы действовать Квантик и Ноутик, чтобы фокус всегда удавался.

39.
а) На одной из сторон прямоугольника выбрали любую точку и соединили с вершинами противоположной стороны. Получился треугольник (синий на рисунке 1). Докажите, что площадь этого треугольника равна половине площади прямоугольника.
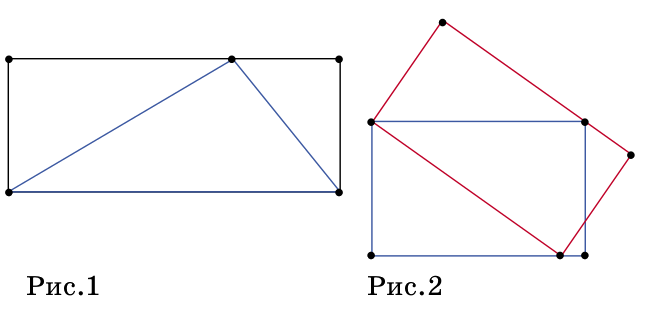 б) На рисунке 2 изображены два прямоугольника – один нарисован синим карандашом, а другой – красным. Докажите, что площади этих прямоугольников равны.
б) На рисунке 2 изображены два прямоугольника – один нарисован синим карандашом, а другой – красным. Докажите, что площади этих прямоугольников равны.
40. Пока Лиза и Вова, стоя на эскалаторе метро, поднялись наверх, их неутомимый друг Квантик на спор успел подняться, спуститься и снова подняться по этому же (едущему вверх) эскалатору. Бежал Квантик всё время с одной и той же скоростью. Во сколько раз эта скорость больше скорости эскалатора?
VII тур

31.(Григорий Гальперин)
а) На большом клетчатом листе бумаги нарисовали «по клеточкам» квадрат 100 x 100 клеток.
Сколько клеток к нему примыкает снаружи (соприкасается с ним хотя бы по вершине)?
б) Сказочный замок имеет форму
большого куба, склеенного из одинаковых маленьких кубиков. Внутри
замка часть кубиков убрали, и получилась пустая комната размерами
10 x 10 x 10 кубиков. Сколько кубиков примыкает снаружи к этой
комнате (соприкасается с ней хотя бы по вершине)?

32. На входе в школу появилось объявление: «Директор школы категорически возражает против отмены решения о запрете контроля за причёсками». Может ли теперь Вася покрасить волосы в красный цвет без риска получить наказание от директора и почему?

33.(Павел Кожевников) Нарисуйте фигуру с девятью сторонами, которую можно разрезать на три треугольника (и покажите, как сделать такое разрезание).
34.(Павел Кожевников)
Барон Мюнхгаузен приехал к Квантику и Ноутику в гости и рассказал:
 – Однажды я встретил 15 детей и заметил, что у любых трёх из них вместе ровно 10 монет. Ответьте-ка, сколько
монет у всех этих детей вместе?
– Однажды я встретил 15 детей и заметил, что у любых трёх из них вместе ровно 10 монет. Ответьте-ка, сколько
монет у всех этих детей вместе?
– Это легко, – сказал Ноутик, – детей можно разделить
на пять троек, а значит, всего монет 50.
– А я думаю, барон что-то путает, – сказал Квантик.
Кто прав – Квантик или Ноутик?
35. В наборе из 100 гирек любые две гирьки отличаются по массе не более чем на 20 г. Имеются чашечные весы, показывающие разность весов на чашах. Придумайте алгоритм, как разложить гирьки на две кучи, чтобы в каждой куче было по 50 гирек и чтобы масса первой кучи отличалась от массы второй кучи тоже не больше чем на 20 г (и докажите, что ваш алгоритм верный).
VI тур

26. Можно ли умножить число 101001000100001 на другое целое число так, чтобы среди цифр произведения не было нуля?

27. (Григорий Гальперин) Сто одинаковых шкатулок расположены в один ряд. В одной из шкатулок находится бриллиант. На каждой шкатулке сделана надпись: «Бриллиант лежит в соседней шкатулке(слева или справа)». Известно, что ровно одна надпись из ста правдивая, а все остальные – ложь. Разрешается открыть ровно одну из шкатулок. Можно ли открыть такую шкатулку, чтобы после этого точно узнать, где лежит бриллиант?
28.
а) Каким наименьшим числом прямых можно разрезать все клетки доски 3x3? Нарисуйте такие прямые и докажите, что меньшим числом прямых обойтись нельзя. (Чтобы клетка была разрезана, прямая должна проходить через внутреннюю точку этой клетки.)
б) Та же задача для доски 4x4.

29. Петя, Коля и Вася решали задачи из задачника и решили вместе 100 задач, при этом каждый из них решил ровно 60 задач. Будем называть задачу, которую решили все трое, лёгкой, а задачу, которую решил только один из ребят, – трудной. Каких задач было больше, лёгких или трудных, и на сколько?

30.(Павел Кожевников) Тётя Маша купила рулон обоев радиуса 15 см на катушке радиуса 5 см (то есть толщина обоев на катушке равнялась 10 см). Она оклеила обоями половину стен в комнате, и толщина обоев стала равна 5 см (то есть рулон стал радиуса 10 см). «Ну что же, израсходовано полрулона, как раз хватит на вторую половину», – подумала тётя Маша. На какую часть стены на самом деле хватит ей оставшейся части рулона?
V тур

21.(Игорь Акулич) На обложке одного из современных журналов напечатали рекламу: возьмите число из двух последних цифр своего телефона, умножьте на 2, прибавьте 3, умножьте на 4, вычтите 12 и разделите на исходное число. Тот, у кого получилось 8, может получить 2300000 рублей! Оцените, велика ли вероятность попасть в число счастливчиков, которые, согласно рекламе, могут получить заветные 2300000 рублей.
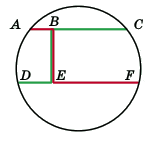
22. (Григорий Гальперин) В круглом парке проложены две параллельные дорожки, соединённые перпендикулярной им перемычкой, как показано на рисунке. Один пешеход прошёл по маршруту ABEF, а второй – по маршруту CBED. Чей путь был длиннее?
23. (Егор Бакаев) Найдутся ли такие 10 натуральных чисел, что ровно одно из них делится на 10, ровно два делятся на 9, ровно три делятся на 8, ровно четыре делятся на 7, ровно пять делятся на 6, ровно шесть делятся на 5, ровно семь делятся на 4, ровно восемь делятся на 3, ровно девять делятся на 2 и ровно десять делятся на 1?

24. Есть 18 камешков, причём известно, что любые два камешка различаются по весу. Как за 25 взвешиваний на двухчашечных весах без гирь найти самый тяжёлый и самый лёгкий камешки?
25. Имеются четыре одинаковые монеты. Используя только их, выложите на столе три монеты в ряд так, чтобы соседние монеты касались, а центры монет были на одной прямой.
IV тур

16. – У Димы больше тысячи книг!
– Да нет, у него меньше тысячи книг.
– Ну уж хотя бы одна-то книга у него точно есть.
Известно, что среди этих утверждений ровно одно
верное. Сколько книг может быть у Димы? Укажите
все возможные варианты.
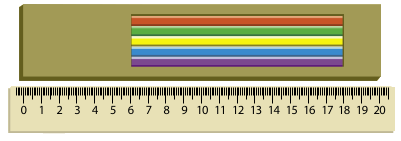
17. (Алексей Воропаев) Квантик купил коробочку с окошком, в которой вплотную другу к другу были уложены карандаши (как на рисунке). Квантик вертел коробочку и так и сяк, но карандаши всегда закрывали всё окошко целиком. Значит ли это, что карандаши длиной со всю коробку? Или они могут быть короче, и тогда какова их минимальная длина?

18. (Егор Бакаев) В конце учебного года шестиклассник Ваня посчитал количество замечаний в своём дневнике за 6-й класс. Их оказалось 50. Ваня заметил, что с каждым годом количество замечаний возрастает на одно и то же число. Cколько замечаний получит Ваня за все 11 лет учёбы в школе, если эта закономерность будет продолжаться? Укажите все возможные ответы.

19. (Илья Иткин) В середине Сашиной линии метро есть две станции с похожим интерьером: «Зелёная» и «Лесная». Саша раз в месяц ездит на важное занятие на «Лесную» через «Зелёную». Но каждый раз получается так: Саша зачитывается новым номером «Квантика», не слышит объявлений диктора и оказывается перед дверями вагона, которые через несколько секунд закроются, не зная, где он – на «Зелёной» или на «Лесной». Как лучше поступать Саше, чтобы в среднем он тратил меньше времени: выходить или ехать до следующей станции? Поезда ходят в обе стороны с промежутком в 3 минуты, время в пути между соседними станциями – тоже 3 минуты.
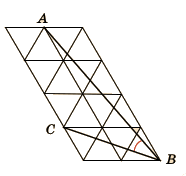
20. (Никита Медведь) На бумаге «в треугольную клеточку» нарисован рисунок. Найдите величину угла ABC. (У треугольников-клеточек все углы равны по 60°. При решении вам может пригодиться такой факт: сумма углов любого треугольника равна 180°.)
III тур

11. Может ли так быть, что к числителю дроби прибавили 1, к знаменателю прибавили 10, а дробь от этого увеличилась? (Числитель и знаменатель дроби – целые положительные числа).

12.
Плитка склеена из трёх равносторонних треугольников со стороной 1 см и имеет
форму четырёхугольника со сторонами 1 см,
1 см, 1 см, 2 см. Можно ли такими плитками замостить равносторонний треугольник
со стороной
 а) 9 см;
а) 9 см;
б) 10 см?
13. (Егор Бакаев) За завтраком 7 гномов сидели за круглым столом. За обедом они хотят сесть за этот же стол так, чтобы количество сидящих между каждыми двумя гномами поменялось. Получится ли у них это сделать?

14. (Николай Константинов) Десять человек пришли в гости в шляпах. Уходили они по одному, и каждый надевал любую шляпу, которая на него налезала. Если такой шляпы не было, то гость уходил без шляпы. Какое наибольшее число гостей могло уйти без шляп?

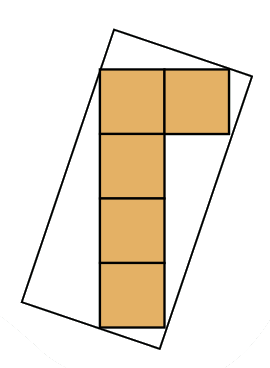
15. (Михаил Евдокимов) Дом имеет форму буквы «Г» из пяти клеток. Вокруг дома построили забор в виде прямоугольника, как показано на схеме внизу. Что больше внутри забора: площадь, занимаемая домом, или площадь, свободная от дома?
II тур

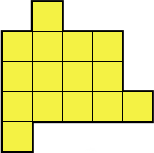
6. (Юрий Маркелов, ученик 5 кл.) Разрежьте фигуру на рисунке на три равные части.
7. (Андрей Меньщиков) Семиклассник Коля считает семизначное число интересным, если его сумма цифр делится на 7. Коля утверждает, что двух подряд идущих интересных семизначных чисел не существует. Не ошибается ли он?

8. (Григорий Гальперин)
Какое число больше и во сколько раз:
A=(1-1/2)(1/3-1/4)(1/5-1/6)...(1/97-1/98)(1/99-1/100)
или
B=(1/2-1/3)(1/4-1/5)(1/6-1/7)...(1/96-1/97)(1/98-1/99)?

9. (Григорий Фельдман и Дмитрий Баранов) На листке бумаги нарисован угол. Квантик хочет проверить, острый этот угол или нет, имея в распоряжении только циркуль. Как ему сделать это, проведя всего одну окружность?
10. (Егор Бакаев)
а) Во дворе 16 ребят водили хоровод. У каждого в хороводе было ровно три друга – те, с кем он держался за руки, и тот, который стоял напротив. Одного из ребят мама позвала обедать, и он убежал домой. Смогут ли остальные встать в хоровод так, чтобы за руки держались друзья?
б) А если бы хоровод водили 18 ребят?
I тур

1. Три бобра построили плотину за 12 дней. Весной её смыло, бобры позвали соседей и отстроили плотину за 4 дня. Сколько соседей позвали бобры?
2. (Сергей Дворянинов) На доске написаны все натуральные числа от 1 до 2015 – некоторые числа красным маркером, а остальные – синим. Наибольшее синее число равно количеству синих чисел, наименьшее красное число – в два раза меньше количества красных чисел. Сколько красных чисел написано на доске?
3.(Андрей Меньщиков) Карлсон поставил на шахматную доску несколько фишек (в каждую клетку – не более одной), причём на каждой горизонтали и вертикали оказалось не менее двух фишек. Всегда ли Малыш может убрать несколько из них так, чтобы на каждой горизонтали и вертикали осталось ровно по одной фишке?
4.(Сергей Дворянинов) У нас во дворе растут две берёзы и две рябины. Когда Вася смотрит из своего окна, то он видит две берёзы, стоящие между двумя рябинами. Когда Петя смотрит из своего окна, то он видит две рябины, стоящие между двумя берёзами. Как такое может быть?

5.(Павел Кожевников) Квантик заинтересовался, верна ли такая теорема: Пусть даны два многоугольника, имеющие равные площади. Тогда один из них можно разрезать на 10 частей и сложить из них другой многоугольник. Помогите Квантику разобраться.
